(自学笔记5)线性回归模型回归系数的解读
本文仅用于自学,文字内容根据视频整理,侵删。
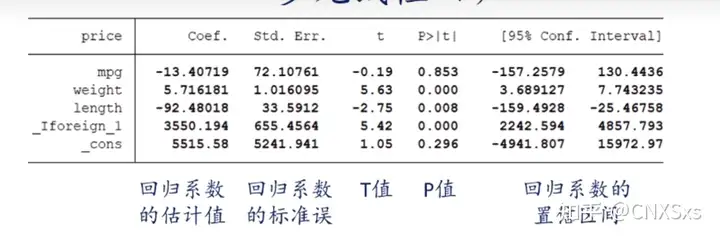
通常在做实证的时候stata跑出来以上的结果。我们通常只需要根据系数正负号判断影响方向,以及根据P值判断显著性即可。不过有的时候,我们也需要在文章中去解释我们回归系数的经济意义。这也是这篇笔记的由来。
一、回归系数的估计值:连续型变量。
当自变量x为连续型变量时,其系数β1的解释为:当其他自变量不变时,自变量x每增加一个单位,因变量y会变化β个单位。如上图mpg,系数为-13.4,则说明,mpg每增加一个单位,因变量price就会减少13.4元。
二、0、1变量
当自变量x为0或1变量时,其系数β2的解释为:当其他自变量不变时,自变量x取值为1时,因变量y会变化β2个单位。如上图foreign取值为1时,则二手车取值为外国车时,因变量price会增加3550.194元。
三、当取对数时
1.自变量和因变量均为对数(log-log model)
如果把其看作一个整体,则是lnx每增加1个单位,lny增加β个单位。但是这样的解释是不可以的。应对x求偏导。结果解读应为:当其他变量不变时,自变量x增加1%,因变量y变化1%β个单位。

2.因变量取对数、自变量为连续型变量(log-linear model)

结果解读应为:当其他变量不变时,自变量x增加1,因变量y增加100%*β个单位。
3.自变量取对数(linear-log model)

结果应解读为:当其他变量不变时,自变量x增加1%,因变量变化0.01*β个单位。
四、回归系数的经济解读
自变量可以分为:分类型自变量(0-1)、计数型自变量(不能取负数,一般不取小数)、连续型自变量
当自变量为分类型(0-1)变量时,回归结果可以解释为:不同分组的因变量平均值差值。

当自变量为计数型变量时,回归结果可以解释为:次数或者个数增加1,因变量取值增加β

当自变量为连续型变量时,自变量增加一个单位,因变量增加β。
但同时,自变量和因变量的取值范围往往也会影响其经济意义(具体请看下面这个视频的例子,非常好)
所以,一个很好的解释经济意义的方法是,用标准差衡量,即自变量每增加一个标准差,因变量会增加β*标准差的值。该增加量占因变量平均值的【XXX】。(划重点)!


其实视频中,没有讨论到一个现实中更常见的问题,当自变量为0-1变量,因变量取对数时(大多数did的文章),该如何解释系数的意义。后面我在公众号搜到了答案。(懒得打字,看图吧)
