(自学笔记12)为了给老板打工学了QCA
零、前置知识
- 逻辑组合数量=$2^n$,n为条件变量数量,当n=1时,条件变量x分为高水平x和低水平~x,以此类推。
- 逻辑符号:source:b站up主:加菲那个猫屋
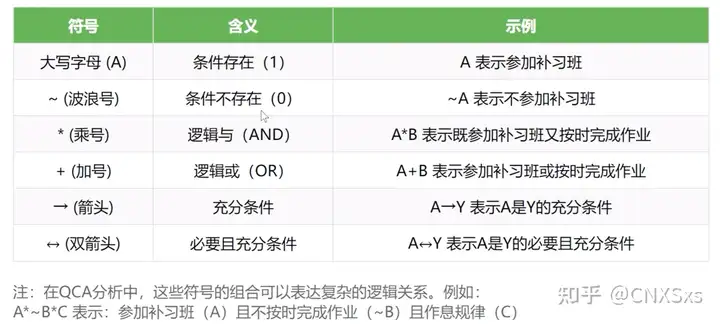
- QCA的非对称思维:传统对称思维假设高投入导致成功,那么低投入则会导致失败;而QCA非对称思维则会探讨成功和失败各自的路径,比如高投入×强学习能力导致成功,而低合作×弱创新文化导致失败。
一、QCA理论入门
e.g. 例如去研究个人特点和恋爱次数的关系,传统线性回归会找x因素去用最小二乘法拟合预测曲线,例如身高越高,恋爱次数越多。而QCA研究的是组态关系,去研究身高、长相、金钱等多种因素相互作用下对恋爱次数的影响关系。
理论解释:QCA,qualitative comparative analysis,定性比较分析,是一种结合定性与定量方法的社会科学研究工具,主要用于分析复杂因果关系中多个条件的组合如何导致特定结果。它通过布尔代数逻辑,揭示不同条件组合的充分性或必要性,尤其适用于中小样本研究(通常10-50个案例)。其主要分为清晰集QCA(csQCA)[严格的二分变量]、多值集QCA(mvQCA)[离散多值变量]、模糊集QCA(fsQCA)[0-1之间的连续模糊集]【Deepseek提供】
目前还有一个增强版的fsQCA,目前我还未深入研究这个(通过R语言实现)
按照数据特征分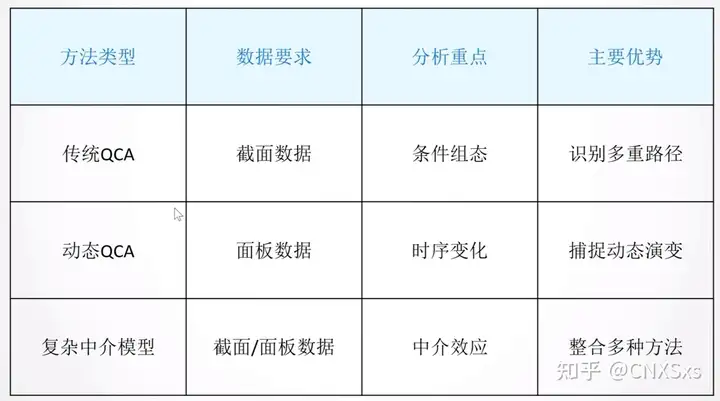
QCA与线性回归的区别
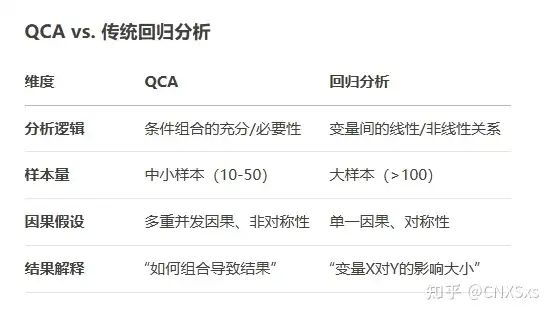
QCA的重要特点
- 因果非对称性:别的因素也可能达到一样的效果。
- 殊途同归:达到目标可以有多条路径。
二、QCA的一般步骤
- 研究问题的确定:是否为对因果关系的探讨。
- 案例的选择:基于主观观察和理论基础,选择合理的案例
- 条件变量和结果变量的选取:条件变量通常为4-7个,考虑可获取性和理论基础。
- 校准:将原始数据转换为符合QCA逻辑的形式的关键步骤
| 校准类型 | 适用场景 | 数据形式 | 校准方法 | 示例 |
|---|---|---|---|---|
| 清晰集校准 | 条件与结果为二分类(存在/不存在) | 布尔值(0或1) | 设定明确阈值,高于阈值设为1,否则为0 | 民主国家:选举自由指数≥7 → 1;<7 → 0 |
| 模糊集校准 | 条件与结果为连续或模糊概念 | 隶属度分数(0到1之间) | 定义完全隶属(1)、交叉点(0.5)、完全不隶属(0)的阈值,使用S型或线性函数转换 | 经济高增长:增长率≥8% → 1;=5% → 0.5;≤2% → 0 |
| 多值集校准 | 条件有多个离散类别(如低、中、高) | 多值编码(如1, 2, 3) | 根据理论或数据分布划分区间,每个区间对应特定值 | 教育水平:文盲率>30% → 1(低);10-30% → 2(中);<10% → 3(高) |
必要性分析:用于确定某个条件(或条件组合)是否是结果发生的必要条件。必要条件意味着,当结果发生时,该条件必须存在(即“无此条件,结果必不出现”),通常一致性水平>0.9是必要条件。并且在一致性水平较高情况下,去看覆盖度才是有意义的。
充分性分析:旨在识别导致结果发生的充分条件组合,即某一条件或条件组合存在时,结果必定(或高概率)发生。充分条件意味着“如果条件存在,则结果发生”(X→Y),但结果的发生可能有其他路径。并且在一致性水平较高情况下,去看覆盖度才是有意义的。
在充分性分析中,覆盖度被分为了原始覆盖度(该条件组态单独解释的结果比例),唯一覆盖度(仅由该条件组态独特解释的结果比例)和总体覆盖度(所有条件组态共同解释的结果比例)三种
| 对比维度 | 充分性分析 | 必要性分析 | 共同点 |
|---|---|---|---|
| 逻辑关系 | X→Y(条件存在→结果发生) | Y→X(结果存在→条件存在) | 均基于集合论与布尔逻辑 |
| 分析目标 | 识别导致结果的充分条件组合 | 识别结果发生的必要条件 | 揭示条件与结果的因果关系 |
| 一致性公式 | 使用相同的数据结构(隶属度) | ||
| 覆盖度意义 | 条件组合对结果案例的覆盖范围 | 条件在结果案例中的普遍性 | 反映解释力的广度 |
| 典型阈值 | 一致性≥0.75,覆盖度无固定标准 | 一致性≥0.9 | 需结合理论与数据确定阈值 |
| 应用场景 | 探索多重因果路径(如企业成功的不同模式) | 确定基础前提(如民主化的必要条件) | 结合使用以全面解释复杂现象 |
| 因果方向 | 条件→结果 | 结果→条件 | 均需明确因果逻辑 |
| 解释焦点 | “如何组合导致结果” | “结果发生必须有什么条件” | 互补分析,构建完整因果链条 |
| 示例 | 高研发+灵活管理→创新成功 | 教育普及←民主化 | 均需校准数据并验证理论合理性 |
组态分析:哪几种条件组合是实现路径。
稳健性检验:集合论检验方式(改变一致性阈值、改变频率阈值、改变PRI阈值),其他检验方式(更换校准锚点,提高校准锚点)
三、QCA实证结果与分析
软件:fsQCA
- 导入数据
- 校准数据:点击Variables-compute variable-calibrate,点击需要校准的数据,在target variable输入校准后生成的变量名,如calibrate(y,n1,n2,n3),其中n1表示完全隶属,n2表示交叉点,n3表示完全不隶属,也就是根据数据的分位排序选择对应水平,比如90%表示完全隶属。
如何找到对应的分位点,使用excel的percentile函数,=percentile(c2:c30,0.95)
导出数据,并对数据为0.5的改成0.501或者0.499,因为当50%为交叉点时,数据为0.5刚好处于交叉点上,无法判断该数据为完全隶属还是完全不隶属。
必要条件分析:点击analyze-necessary conditions-点击outcome选择结果变量-在add condition中将是或非的结果变量(a1,~a1)都加入其中-生成结果(consistency表示必要性的一致性水平,coverage表示覆盖度)-当一致性水平>0.9时,通常认为是必要条件,但此时还应该对该变量进行检验(fsQCA软件无法实现)
充分性分析:点击analyze-truth table-outcome选择结果变量-在causal condit选择条件变量-生成的真值表中number表示:在原有案例中,有多少案例拥有这样一个条件组态(百分比表示案例的累计百分比)-结果变量此时为空值,需要对其进行编码-raw consist. 充分性的一致性水平-PRI consist. PRI的一致性水平-SYM consist. 对称一致性水平
充分性阈值选取:点击edit-Delete rows width number,输入频数的阈值,也就是希望条件组态至少能被多少案例所覆盖(小样本可以选择1)-set outcome to 1 for rows with consist. 选择阈值
PRI一致性:将低于阈值水平(如0.7)的outcome手动编码为0
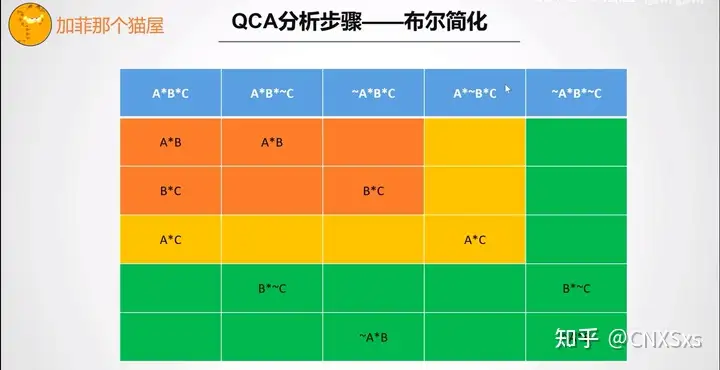
标准分析:点击右下角standard analyses-布尔简化步骤-对中间解的容易反事实分析部分进行判断-
QCA的三种解【内容由Deepseek】生成
简单解(Parsimonious Solution):通过布尔代数最大程度简化条件组合,仅保留核心条件,删除所有冗余或辅助条件。纳入所有的逻辑余项
示例:企业创新成功的简单解:创新成功=高研发投入+灵活管理
复杂解(Complex Solution):保留所有可能的条件组合,不进行任何简化,完全依赖数据驱动。不纳入任何逻辑余项。
示例:企业创新成功的复杂解:创新成功=高研发投入⋅灵活管理+高研发投入⋅政策支持+灵活管理⋅市场机遇
中间解(Intermediate Solution):在简单解与复杂解之间平衡,结合数据与理论假设,通过合理反事实分析生成更贴近实际的解。基于理论预期处理逻辑余项【大多数研究的最优选择】
示例:企业创新成功的中间解:创新成功=高研发投入⋅灵活管理+政策支持⋅市场机遇
感兴趣的去看up的讲解吧,讲的很不错,我这里只是自学记录用。
结果解读:会生成三种解的结果。unique coverage唯一的覆盖度:表示在成功的案例中,仅能被这个组态所解释的比例(清晰集的解释)-solution coverage 解的总体的覆盖度- solution consistency 解的总体的一致性
结果汇报:当简单解和中间解同时存在或同时缺失时,就是核心存在或核心缺失;当只有中间解存在或缺失时,就是边缘存在或边缘缺失。
动态QCA
分析步骤是类似的,但是由于加入了时间趋势,需要考虑组间和组内的结果。
pooled consistency表示汇总的一致性
pooled coverage表示汇总的覆盖率
between to pooled表示组内或组间一致性的差异